Calculer une moyenne est une compétence fondamentale que tout le monde doit maîtriser, que ce soit pour les études, le travail ou même dans la vie quotidienne. Dans cet article, nous allons vous expliquer, de manière claire et détaillée, comment calculer une moyenne. Nous couvrirons les différentes méthodes de calcul, les contextes dans lesquels ces calculs sont utilisés, et répondrons aux questions fréquemment posées à ce sujet.
Comment calculer une moyenne?
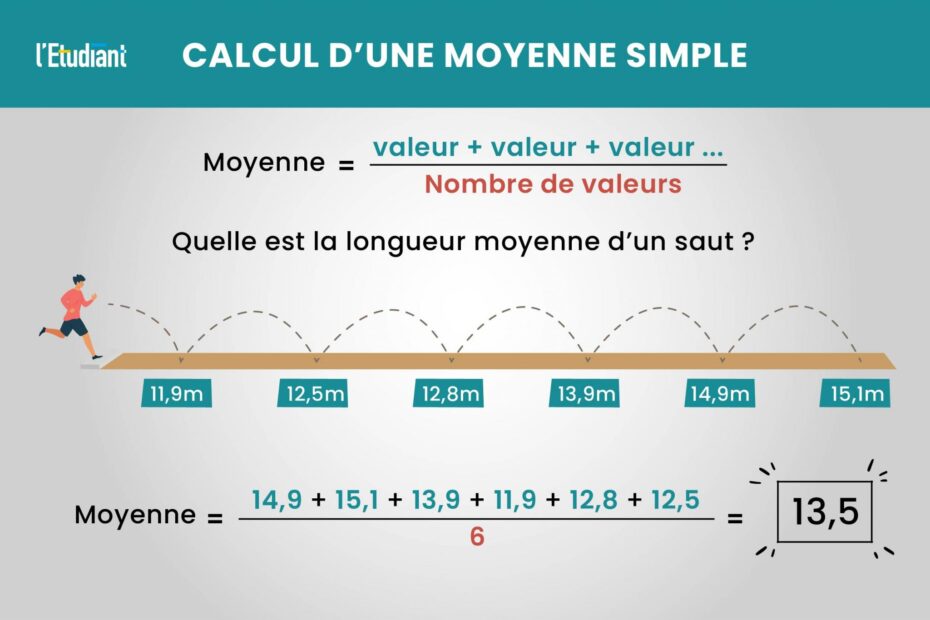
Pour calculer une moyenne, additionnez toutes les valeurs d’un ensemble de données et divisez le total par le nombre de valeurs. Cette méthode permet de déterminer la tendance centrale de ces données.
Qu’est-ce qu’une moyenne?
Avant de calculer une moyenne, il est important de comprendre ce qu’elle représente. La moyenne est une mesure statistique qui permet de résumer un ensemble de données en une seule valeur. Elle donne une idée générale de la tendance centrale d’un groupe de chiffres.
Il existe plusieurs types de moyennes, mais la plus courante est la moyenne arithmétique, que nous allons aborder dans cet article.
Comment calculer une moyenne arithmétique?
La moyenne arithmétique est la somme de tous les éléments d’un ensemble de données, divisée par le nombre d’éléments dans cet ensemble. Voici la formule :
Moyenne = (Somme des valeurs) ÷ (Nombre de valeurs)
Exemple de calcul de la moyenne
Supposons que vous ayez les notes suivantes dans un examen : 12, 14, 10, 18 et 16. Pour calculer la moyenne, suivez ces étapes :
- Additionnez les valeurs :
12 + 14 + 10 + 18 + 16 = 70 - Divisez la somme par le nombre de valeurs :
70 ÷ 5 = 14
Donc, la moyenne des notes est 14.
Étapes pour calculer la moyenne
Voici un résumé des étapes pour calculer une moyenne :
- Additionnez toutes les valeurs.
- Divisez le total par le nombre d’éléments.
C’est aussi simple que cela ! Mais attention, dans certains cas, la moyenne peut ne pas être suffisante pour donner une image complète des données. Nous verrons plus tard comment la pondération et d’autres techniques peuvent influencer ce calcul.
Moyenne pondérée : une variante importante
Dans certains cas, vous devrez calculer une moyenne pondérée. Cela se produit lorsque chaque valeur de l’ensemble de données a une importance différente. Au lieu de donner le même poids à chaque valeur, vous appliquez un coefficient (ou poids) à chaque valeur avant de faire la somme et de diviser par la somme des poids.
La formule de la moyenne pondérée est la suivante :
Moyenne pondérée = (Somme des valeurs × poids) ÷ (Somme des poids)
Exemple de moyenne pondérée
Supposons que vous ayez trois notes : 12, 14 et 18, avec des poids respectifs de 1, 2 et 3. Le calcul de la moyenne pondérée serait :
- Multiplier chaque note par son poids :
12 × 1 = 12
14 × 2 = 28
18 × 3 = 54 - Additionner les résultats :
12 + 28 + 54 = 94 - Additionner les poids :
1 + 2 + 3 = 6 - Diviser la somme des produits par la somme des poids :
94 ÷ 6 = 15.67
Donc, la moyenne pondérée des notes est 15,67.
Moyenne géométrique : un autre type de moyenne
La moyenne géométrique est utilisée lorsque les valeurs de l’ensemble de données sont multipliées ou liées de manière exponentielle, comme dans le cas des taux de croissance ou des rendements financiers. Contrairement à la moyenne arithmétique, qui est basée sur la somme des valeurs, la moyenne géométrique est basée sur le produit des valeurs.
La formule de la moyenne géométrique est la suivante :
Moyenne géométrique = (Produit des valeurs)^(1/n)
où n est le nombre de valeurs.
Exemple de moyenne géométrique
Imaginons que vous ayez les chiffres suivants : 2, 4 et 8. Pour calculer la moyenne géométrique :
- Multipliez les valeurs :
2 × 4 × 8 = 64 - Prenez la racine n-ième du produit :
(64)^(1/3) = 4
Donc, la moyenne géométrique de 2, 4 et 8 est 4.
Moyenne harmonique : pour des valeurs inverses
La moyenne harmonique est une autre méthode de calcul de la moyenne qui est utilisée lorsque vous travaillez avec des valeurs inverses, comme dans le cas des vitesses moyennes ou des rendements de certains investissements. Contrairement à la moyenne arithmétique, qui donne un poids égal à chaque valeur, la moyenne harmonique donne plus de poids aux valeurs faibles.
La formule de la moyenne harmonique est la suivante :
Moyenne harmonique = n / (1/x₁ + 1/x₂ + … + 1/xn)
Exemple de moyenne harmonique
Supposons que vous ayez les vitesses suivantes : 60 km/h, 90 km/h et 120 km/h. Pour calculer la moyenne harmonique :
- Calculez les inverses des valeurs :
1/60 = 0,01667
1/90 = 0,01111
1/120 = 0,00833 - Additionnez les inverses :
0,01667 + 0,01111 + 0,00833 = 0,03611 - Divisez le nombre de valeurs par la somme des inverses :
3 ÷ 0,03611 = 83,04
Donc, la moyenne harmonique des vitesses est 83,04 km/h.
Pourquoi calculer une moyenne?
Le calcul d’une moyenne peut être utile dans divers contextes. Voici quelques exemples où la moyenne joue un rôle important :
- En éducation : Les enseignants utilisent les moyennes pour évaluer les performances des élèves, en calculant la moyenne des notes.
- En économie : Les économistes calculent des moyennes pour analyser des indicateurs économiques comme le PIB ou le revenu moyen.
- En sport : Les entraîneurs peuvent utiliser la moyenne des performances des joueurs pour évaluer leur niveau.
- En santé : Les médecins utilisent des moyennes pour évaluer les résultats des tests médicaux ou des traitements.
FAQ : Questions fréquentes sur le calcul des moyennes
Quelle est la différence entre la moyenne arithmétique et la moyenne pondérée?
La moyenne arithmétique est la somme de toutes les valeurs divisée par le nombre de valeurs. La moyenne pondérée tient compte du poids de chaque valeur dans l’ensemble de données, ce qui signifie que certaines valeurs peuvent avoir plus d’importance que d’autres.
Comment la moyenne géométrique est-elle différente de la moyenne arithmétique?
La moyenne géométrique est utilisée pour des ensembles de données dont les valeurs sont multipliées ou exponentielles. Elle donne une meilleure mesure de la tendance centrale dans ces cas-là, tandis que la moyenne arithmétique est plus générale et adaptée aux données qui s’additionnent.
Quand utiliser la moyenne harmonique?
La moyenne harmonique est utile lorsque les valeurs représentent des taux ou des vitesses, par exemple dans des calculs liés à des rendements financiers ou des vitesses moyennes.
Pourquoi la moyenne est-elle parfois trompeuse?
Dans certains ensembles de données, surtout si elles comportent des valeurs extrêmes (très élevées ou très faibles), la moyenne peut ne pas refléter correctement la tendance centrale. C’est pourquoi, dans ces cas, d’autres mesures comme la médiane peuvent être plus appropriées.
La moyenne est-elle toujours représentative des données?
Non, la moyenne n’est pas toujours la meilleure mesure de la tendance centrale, surtout si les données sont très dispersées ou contiennent des valeurs extrêmes. Dans de tels cas, il est souvent préférable d’utiliser la médiane ou d’autres mesures.
Conclusion
Calculer une moyenne est une compétence essentielle dans de nombreux domaines. Que vous calculiez une moyenne arithmétique, pondérée, géométrique ou harmonique, comprendre quand et comment utiliser chaque type de moyenne peut grandement améliorer votre analyse des données. N’oubliez pas que, bien que la moyenne soit une mesure utile, elle ne reflète pas toujours fidèlement l’ensemble des données, en particulier si elles sont fortement dispersées.
En maîtrisant ces différentes techniques de calcul de la moyenne, vous serez bien équipé pour tirer des conclusions précises et informées à partir de vos données.