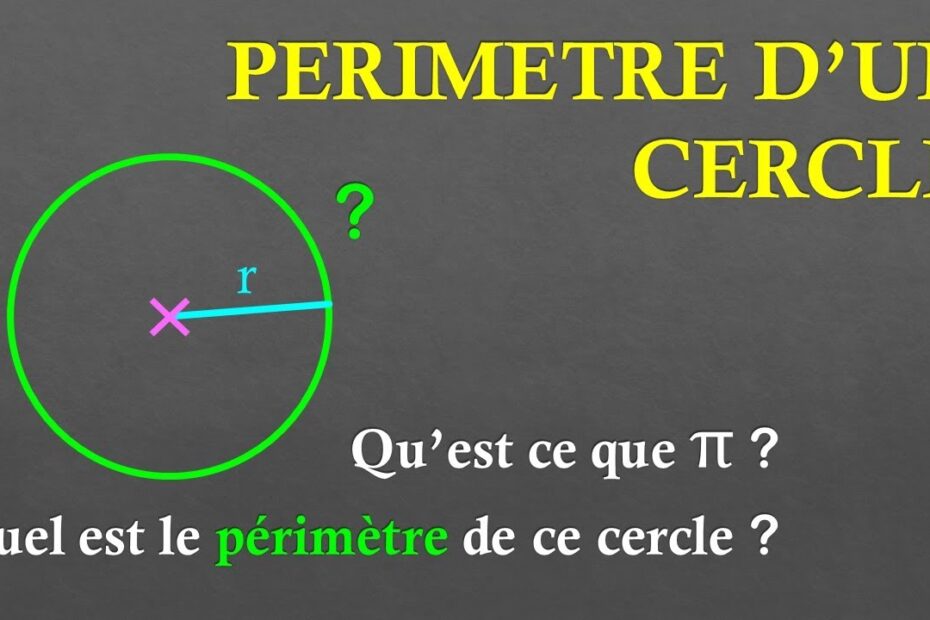
Calculer le périmètre d’un cercle est une opération simple, mais essentielle pour de nombreuses applications en mathématiques, en physique et dans la vie quotidienne. Le périmètre d’un cercle, également appelé circonférence, peut être facilement calculé en utilisant une formule bien connue. Dans cet article, nous allons vous expliquer tout ce que vous devez savoir pour comprendre et effectuer ce calcul, étape par étape.
Qu’est-ce que le périmètre d’un cercle ?
Le périmètre d’un cercle est la distance autour du cercle, c’est-à-dire la longueur de la frontière qui délimite le cercle. Cette distance est aussi appelée circonférence. Contrairement à un carré ou un rectangle, dont les périmètres sont calculés en ajoutant les longueurs de tous les côtés, le périmètre d’un cercle dépend de son rayon ou de son diamètre.
La formule pour calculer le périmètre d’un cercle
La formule pour calculer le périmètre d’un cercle est la suivante :P=2×π×rP = 2 \times \pi \times rP=2×π×r
P représente le périmètre du cercle, π (pi) est une constante mathématique, et r est le rayon du cercle, c’est-à-dire la distance du centre du cercle à n’importe quel point de sa bordure.
Qu’est-ce que la constante π ?
Le nombre π est une constante qui représente le rapport entre la circonférence d’un cercle et son diamètre. Sa valeur approximative est :π≈3,14159\pi \approx 3,14159π≈3,14159
Cela signifie que, peu importe la taille du cercle, le rapport entre la circonférence et le diamètre sera toujours le même, soit environ 3,14.
Comment utiliser la formule ?
La formule pour calculer la circonférence d’un cercle repose sur deux paramètres : le rayon et π. Voici un exemple détaillé pour mieux comprendre comment utiliser cette formule.
Exemple 1 : Calculer le périmètre d’un cercle avec un rayon donné
Imaginons qu’un cercle ait un rayon de 5 cm. Pour calculer son périmètre, il suffit de multiplier le rayon par 2 et par π.P=2×3,14159×5P = 2 \times 3,14159 \times 5P=2×3,14159×5
Cela donne :P=31,4159 cmP = 31,4159 \, \text{cm}P=31,4159cm
Ainsi, le périmètre du cercle est d’environ 31,42 cm.
Exemple 2 : Calculer le périmètre d’un cercle avec un diamètre donné
Si l’on connaît le diamètre du cercle plutôt que le rayon, il suffit de diviser le diamètre par 2 pour obtenir le rayon, puis d’appliquer la même formule. Par exemple, si un cercle a un diamètre de 10 cm, le rayon est de 5 cm (car 10 ÷ 2 = 5). Le calcul du périmètre sera identique à l’exemple précédent.
Formule alternative
Si vous avez directement le diamètre d du cercle, vous pouvez également utiliser la formule suivante :P=π×dP = \pi \times dP=π×d
Exemple avec un diamètre donné
Prenons un diamètre de 12 cm. En utilisant la formule alternative, nous avons :P=3,14159×12=37,69908 cmP = 3,14159 \times 12 = 37,69908 \, \text{cm}P=3,14159×12=37,69908cm
Le périmètre du cercle est donc d’environ 37,7 cm.
La précision de π
Bien que π soit souvent arrondi à 3,14 dans les calculs simples, il est en réalité un nombre infini et non périodique. Dans les calculs de haute précision, il peut être utile d’utiliser plusieurs décimales de π. Par exemple, 3,14159265358979323846… est la valeur de π à 20 décimales.
Pourquoi utiliser π dans le calcul du périmètre ?
La présence de π dans la formule du périmètre d’un cercle peut sembler étrange au départ, mais elle a un sens profond en géométrie. Le nombre π est le rapport constant entre la circonférence et le diamètre d’un cercle, quel que soit le cercle que l’on examine. Ainsi, il permet de relier la mesure linéaire du rayon ou du diamètre à la mesure de la circonférence, offrant une méthode universelle pour calculer la distance autour du cercle.
Calculer le périmètre d’un cercle avec une calculatrice
Aujourd’hui, pour simplifier les calculs, vous pouvez utiliser une calculatrice scientifique ou même une application de calcul en ligne pour déterminer rapidement le périmètre d’un cercle. Il vous suffit de saisir le rayon ou le diamètre du cercle, puis d’appliquer la formule correspondante.
Pourquoi est-il important de connaître le périmètre d’un cercle ?
Le périmètre d’un cercle est utilisé dans de nombreux domaines pratiques, comme :
- L’ingénierie : Pour concevoir des roues, des tubes, ou des circuits.
- L’architecture : Lors de la création de plans pour des bâtiments ou des structures circulaires.
- La physique : Pour étudier les propriétés des mouvements circulaires ou des objets en rotation.
- Le design : Lors de la création d’objets circulaires comme des horloges, des plaques, ou des motifs décoratifs.
Calculer le périmètre d’un cercle : Questions fréquemment posées
Quelle est la différence entre le rayon et le diamètre d’un cercle ?
Le rayon est la distance entre le centre du cercle et n’importe quel point de la bordure. Le diamètre, quant à lui, est la distance qui relie deux points de la bordure du cercle en passant par son centre. Le diamètre est donc toujours deux fois plus grand que le rayon.
Peut-on calculer la circonférence d’un cercle sans connaître son rayon ?
Oui, il est possible de calculer la circonférence d’un cercle sans connaître directement son rayon, à condition de connaître son diamètre. Dans ce cas, il vous suffit d’utiliser la formule P=π×dP = \pi \times dP=π×d, où d est le diamètre.
Pourquoi est-ce important de connaître le périmètre d’un cercle dans la vie quotidienne ?
Le calcul du périmètre d’un cercle est utilisé dans divers contextes pratiques, comme le calcul de la quantité de matériaux nécessaires pour construire des objets circulaires (par exemple, des tuyaux, des roues, des terrains de sport) ou pour déterminer la distance autour d’un objet rond, comme une clôture ou un jardin circulaire.
Quelle est la formule du périmètre d’un cercle en fonction de son rayon ?
La formule la plus courante pour calculer le périmètre d’un cercle est P=2×π×rP = 2 \times \pi \times rP=2×π×r, où r représente le rayon du cercle. Cela permet de connaître rapidement la circonférence du cercle en multipliant simplement le rayon par deux et par la constante π.
Conclusion
Le calcul du périmètre d’un cercle est une opération fondamentale en géométrie. En comprenant la relation entre le rayon, le diamètre et la constante π, vous pouvez facilement déterminer la circonférence de tout cercle. Que ce soit pour des applications pratiques en ingénierie, en architecture ou dans des contextes quotidiens, la capacité à calculer le périmètre d’un cercle est essentielle. Grâce à la formule simple P=2×π×rP = 2 \times \pi \times rP=2×π×r, vous pouvez résoudre ce calcul rapidement et avec précision.